7034. Portals
Some planets of
the galaxy, where Peter Pyatochkin recently moved, are connected with portals. If
planets A and B are connected, it means that each planet
has a special device – portal – for teleportation between them. The creature
that enters the portal on the planet A, instantly appears on the
planet B and vice versa.
The same portal can not be used to teleport to different planets. If some
pair of planets are not connected yet, they can be united, but a new portal
must be built on each planet. Building portals requires considerable outlay and
can cost differently on different planets.
We say that there
is a teleport way between two planets, if you can get from one planet to
another, teleporting one or more times (using intermediate planets).
Unfortunately, there is no teleportation way between any two planets.
You are given the
communication scheme among the planets and the cost of the portal on each
planet. Determine the lowest amount of money you need to spend to ensure the
existence of a teleportation path between each pair of planets in the galaxy.
Input. The first
line contains two integers: the number of planets in the galaxy n (n ≤
1000) and the number of
planets pairs m, directly connected
with portals.
Second line
contains n positive integers p1, p2,
…, pn – the cost
to build a new portal, respectively on the first, on the second, ...., on the n-th planet. None of the costs
exceed 106.
Each of the next m
lines contains two positive integers ai and bi (1 ≤ ai < bi
≤ n, 1 ≤ i ≤ m) that describe
the pair of connected planets. Each pair is given in input only one time.
Output. Print the
smallest amount of money that should be spent on the portals construction on
some planets so that there would be the teleportation path between each pair of
planets in the galaxy.
|
Sample
input 1 |
Sample
output 1 |
|
4 2 7 4 7 3 1 3 2 4 |
10 |
|
|
|
|
Sample
input 2 |
Sample
output 2 |
|
8 5 3 7 5 7 8 12 6 9 4 5 5 6 8 7 1 2 3 1 |
19 |
SOLUTION
graphs – depth first
search
Algorithm analysis
The input graph
can be disconnected. Find the connected components in it. We’ll build new portals so that they
connect vertices
from different connected components. Moreover, if we initially have k components, then it is enough to build k – 1 new connections to make the graph connected.
Consider two
different connected
components.
To create a transition between them, you need to select a vertex in each of
them and build the
portals. Since it is
more profitable to build a portal in the cheapest vertex, then those should be the
cheapest vertices in each of the connected components. On the other hand, since we
need to connect k different components, the cheapest way is to connect all the components to
the connected component with the cheapest
vertex.
Thus, it is
necessary for each connected component to find the cheapest vertex for building a
portal. Then, among these vertices, find the one that has the lowest cost –
portals leading to all
other connected components will be built in it.
Example
In the first
test, the graph contains two connected components. Next to each vertex, write
down the cost of building a portal in it.
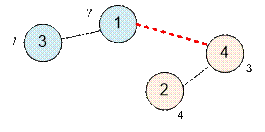
Connect the planets 1 and 4
with portals. The cost of connection is 7 + 3 = 10.
Consider the second test
case.
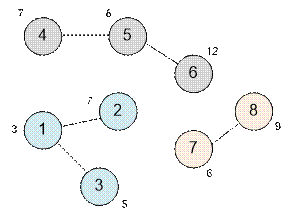
There are three
connected components in total, so it is enough to build two new edges, or 4
portals (2 for each edge). The vertex with number 1 has the lowest cost,
therefore, these two edges will go out from it. And the edges will go to the
vertices of minimum cost in each of other connected components.
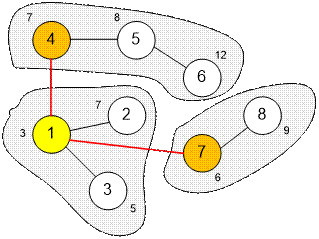
The cost of
connection the
planets is (3 + 7) + (3 +
6) = 19.
Algorithm realization
Declare the arrays. Store the graph
in the adjacency list g. The cost of
building a portal at vertex v is
cost[v]. In mn[i] we’ll store the minimum
cost of building a portal among the vertices of the i-th connected component.
#define MAX 1002
int cost[MAX], used[MAX], mn[MAX];
vector<vector<int> > g;
Depth first search from the
vertex v that belong to cnt-th connected component. Visit all the vertices of the connected component and find the lowest cost
of building a portal in mn[cnt].
void dfs(int
v)
{
used[v] = 1;
mn[cnt] = min(mn[cnt], cost[v]);
for(int i = 0; i < g[v].size(); i++)
{
int to =
g[v][i];
if
(!used[to]) dfs(to);
}
}
The main part of
the program. Read the input
data. Build a graph.
scanf("%d %d",&n,&m);
g.resize(n+1);
for(i = 1; i <= n; i++)
scanf("%d",&cost[i]);
for(i = 1; i <= m; i++)
{
scanf("%d %d",&u,&v);
g[u].push_back(v);
g[v].push_back(u);
}
For each connected component cnt run the depth first search. Find the vertex with the lowest cost to build a portal, and store the found cost in mn[cnt].
for(i = 0; i < MAX; i++) mn[i] =
MAXVALUE;
for(cnt = 0, i = 1; i <= n; i++)
if (!used[i])
dfs(i), cnt++;
In total, graph contains cnt connected components. In the variable temp, we look for the vertex with the
lowest portal construction cost – the minimum among
all values mn[0],…, mn [cnt – 1]. Find the sum of these minimums in the variable res.
int temp = MAXVALUE;
for(res = i = 0; i < cnt; i++)
{
if (mn[i]
< temp) temp = mn[i];
res += mn[i];
}
For example, let the
minimum temp be achieved in the j-th
connected component (temp = mn[j]). Then the
total sum res to build the portals
for all new transitions will be
(mn[j] + mn[0]) + … + (mn[j]
+ mn[j – 1]) + (mn[j] + mn[j + 1]) + …
+ (mn[j] + mn[cnt – 1]) =
= mn[j] * (cnt – 1) + mn[0] +
… + mn[j – 1] + mn[j + 1] + … + mn[cnt – 1] =
= temp
* (cnt – 2) + mn[0] + … + mn[cnt – 1]
res += temp *
(cnt - 2);
Print the answer.
printf("%d\n",res);